Research at the Laboratory of Crystallography

Anisotropic thermal expansion and two-dimensional ferromagnetic clusters in La_n(Ti_1-xFe_x)_nO_3n+2 (n=5 and n=6)
​ 
 

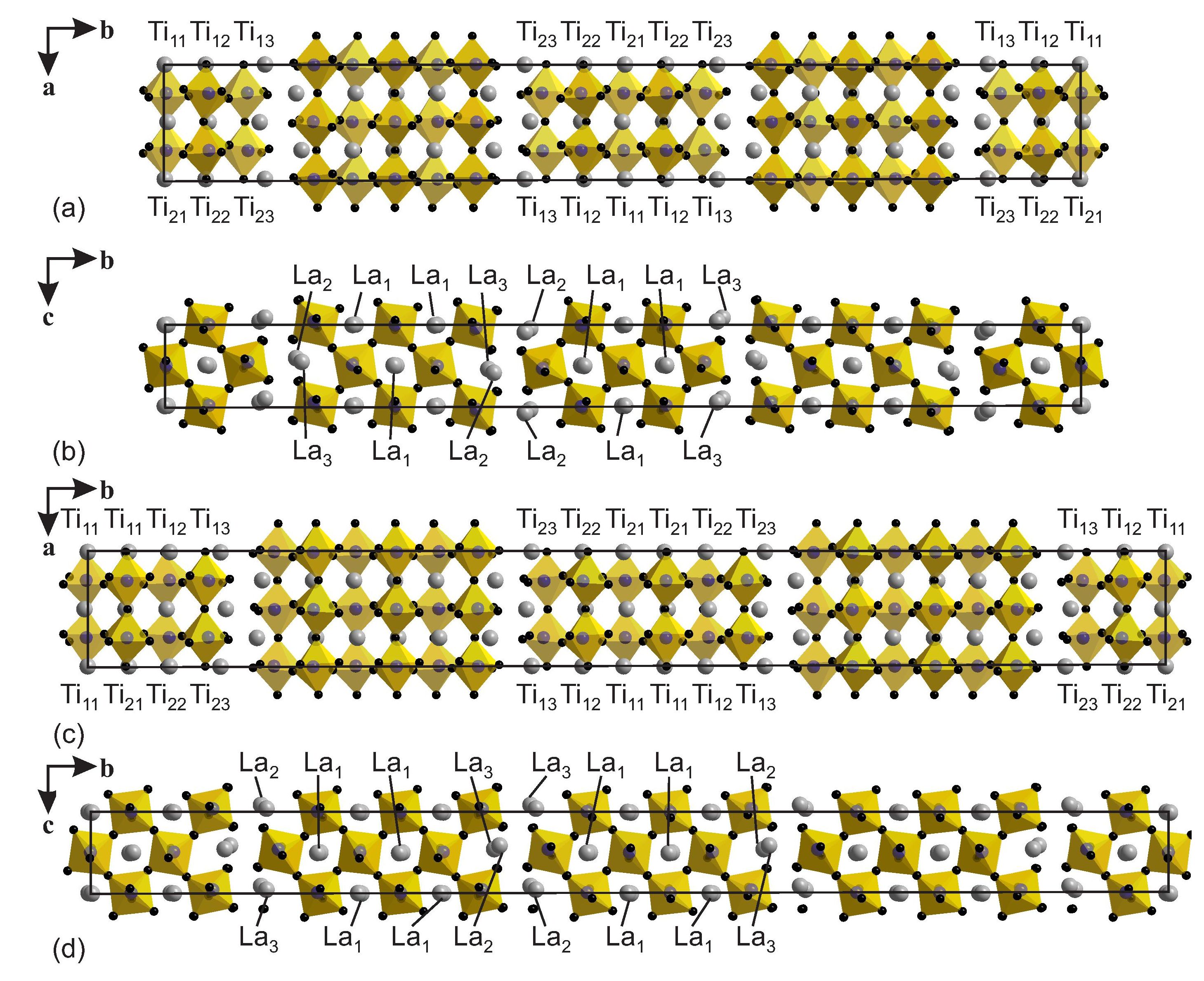
Figure 1: Crystal structures of (a), (b) La₅(Ti_0.8Fe_0.2)₅O₁₇ and (c), (d) La₆(Ti_0.67Fe_0.33)₆O₂₀. Pseudo-orthorhombic supercells are indicated by solid lines. Gray circles represent La atoms and (Ti,Fe)O₆ octahedra are outlined. The numbering denotes the crystallographically independent Ti/Fe and La sites in the supercell description. Reproduced from [1].

La5(Ti0.8Fe0.2)5O17 (n = 5) and La6(Ti0.67Fe0.33)6O20 (n = 6) belong to the homologous series AnBnO3n+2, where A is an alkaline earth or rare earth element, B is a transition metal and 2  < n < 7. The crystal structures comprise slabs of perovskite-type structure of n octahedra thick stacked along b and separated by oxygen-rich layers (Fig. 1).

The homologous series AnBnO3n+2 includes compounds that are high-TC ferroelectric compounds with possible applications in dielectric resonators at microwave frequencies [2]. They include quasi-one-dimensional metals with possible application in resistive memory switching [3]. Incorporation of iron on the B site has resulted in the paramagnetic compounds La5(Ti0.8Fe0.2)5O17 (n = 5) and La6(Ti0.67Fe0.33)6O20 (n = 6) [4].

At high temperatures or as hypothetical high-symmetry structures AnBnO3n+2 compounds possess centrosymmetric orthorhombic symmetries. Ferroelectric or ferromagnetic properties require non-centrosymmetric symmetries. Indeed, accurate single-crystal X-ray diffraction studies have indicated small distortions out of these orthorhombic structures for most of these compounds. The distortions define fourfold superstructures with monoclinic symmetry that is centrosymmetric for n is odd and acentric for n is even.

We have employed single-crystal X-ray diffraction for the determination of accurate crystal structures of n = 5 and n = 6 at seven selected temperatures between 90 and 370 K [1, 5]. The temperature dependence of the crystal structures indicated an anisotropic thermal expansion with the largest expansion parallel to the slabs and the smallest expansion in the stacking direction. This counter intuitive result can be explained by the temperature dependence of the tilts of the (Ti,Fe)O6 octahedral groups [1].

B sites are disorderly occupied by Ti and Fe, with a higher concentration of Fe atoms at sites towards the centers of the slabs. Ti-O and Fe-O bond lengths are expected to be slightly different. This property is nicely demonstrated in the n = 5 and n = 6 compounds by the atomic valences as computed by the Bond-valence method. They indicate that the refined oxygen positions are the average of positions of a TiO6 and positions of a FeO6 octahedron, weighted according to the Ti/Fe occupancies of the site (Fig. 2).
​ 

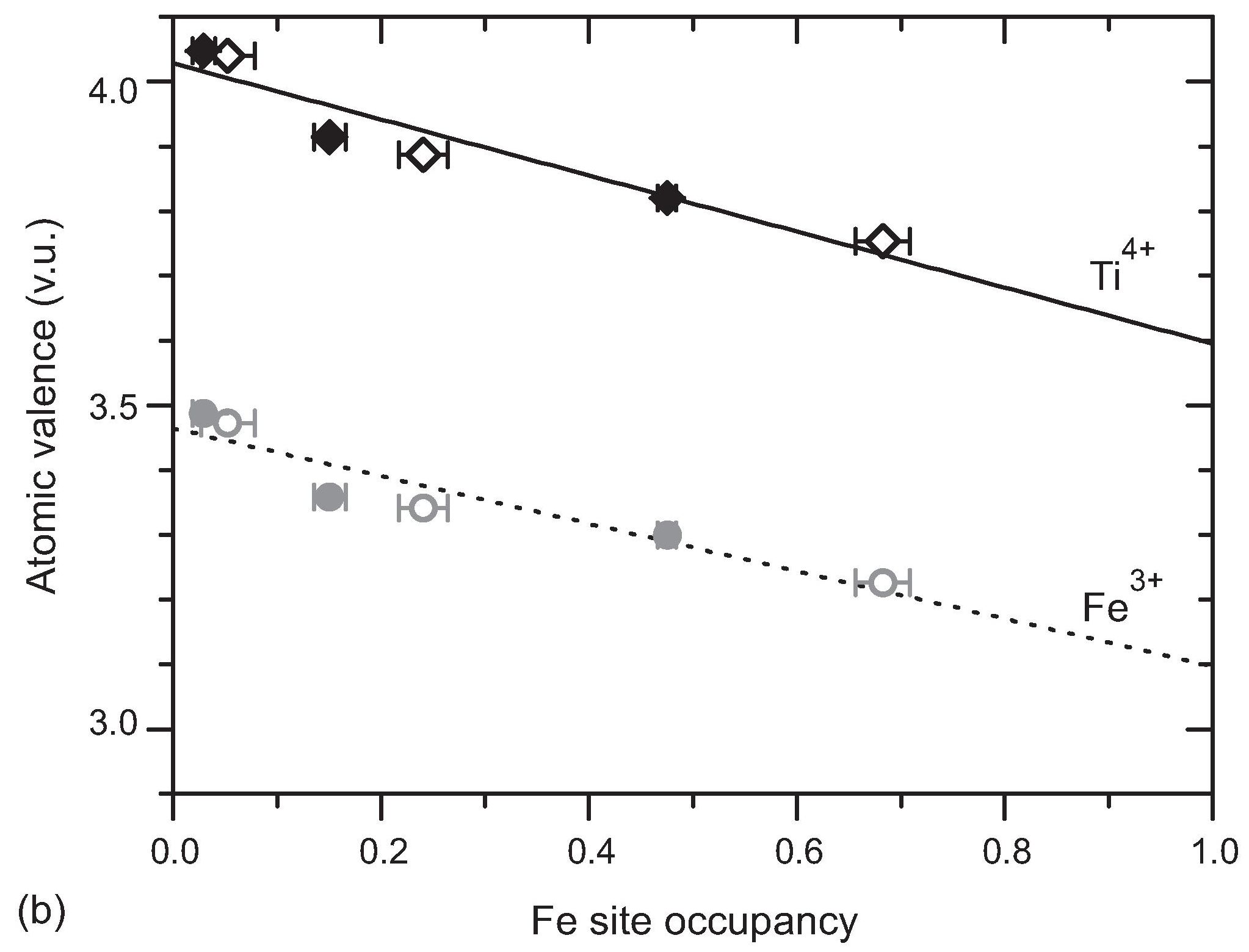
Figure 2: Apparent atomic valences as a function of the site occupancy by Fe. Lines are linear fits to the data, resulting in extrapolated values of V[Ti] = 4.03 (2) for pure Ti sites, and V[Fe] = 3.10 for pure Fe sites. Filled symbols correspond to La5(Ti0.8Fe0.2)5O17; open symbols refer to La6(Ti0.67Fe0.33)6O20. Error bars represent the spread of values for variation of temperature. Reproduced from [1].

Sites Ti13 and Ti23 do not contain Fe and sites Ti12 and Ti22 contain only a small amount of Fe. The spatial arrangements of iron ions can thus be approximated by two-dimensional square lattices with strong magnetic interactions between neighboring sites, albeit with fractional occupancies of the sites Ti11 and Ti21 in Fig. 1(b) by an average of 0.67 magnetic Fe³⁺ ions in n = 6, and by an average of 0.42 magnetic ions on the sites Ti11, Ti12, Ti21 and Ti22 in n = 5 [Fig. (a)].

A previously described (Lichtenberg et al. [4]) crossover of magnetic behavior of n = 6 at room temperature (Fig. 3) is explained by the formation of two-dimensional, ferromagnetically organized magnetic clusters of an average size of 52 Fe³⁺ ions. The absence of long-range magnetic order follows from the fractional occupancy of the sites by magnetic ions. The lower concentration of magnetic ions in n = 5 explains that crossover behavior is not found and clusters do not form in that compound. For a detailed description of the model see [5].
​ 

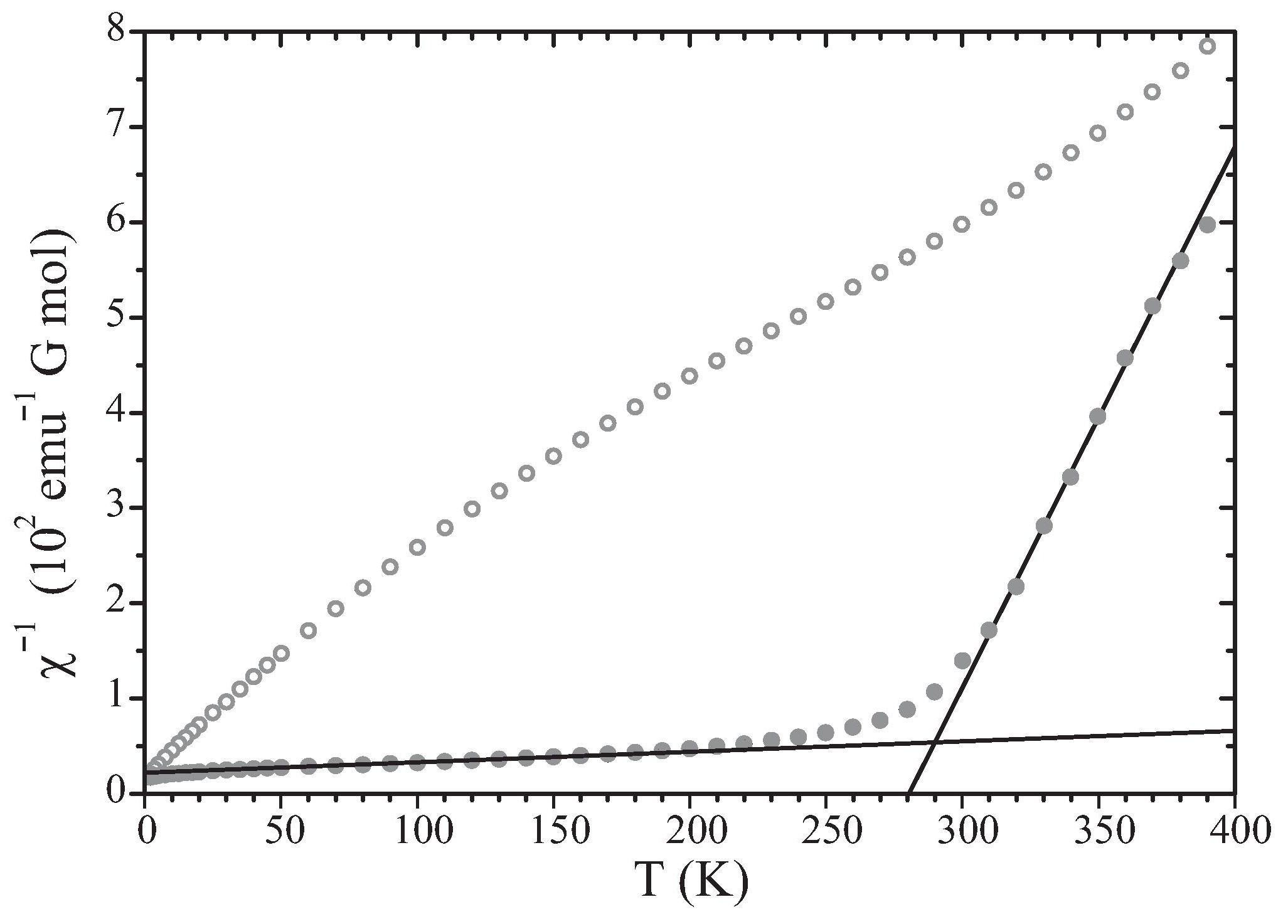
Figure 3: Inverse magnetic susceptibility x^-1 as a function of temperature for n = 5 (open circles) and n = 6 (filled circles). Data reproduced from [4]. Solid lines represent fits of the Curie-Weiss law, &#967^-1 = (T - θ)/C_Curie, to the data of n = 6. For the temperature range of 50-150 K parameters are C_lowCurie = 9.066 emuG^-1Kmol^-1 and θ^low = -196 K; for the temperature range of 310-380 K parameters are C_highCurie = 0.176  emuG^-1K mol^-1 and θ^high = 281 K. These values indicate strong ferromagnetic coupling between Fe³⁺ ions at high temperatures, and antiferromagnetic coupling between ferromagnetic clusters in neighboring slabs below the cross-over temperature. Reproduced from [5].

Participating researchers at the Laboratory of Crystallography in Bayreuth: Alexander Wölfel and Sander van Smaalen.
This research has been done in collaboration with Frank Lichtenberg (Department of Materials, ETH Zurich, 8093 Zurich, Switzerland).
​ 

​​REFERENCES

[1] A. Wölfel, P. Dorscht, F. Lichtenberg, and S. van Smaalen. Anisotropic thermal expansion of La_n(Ti,Fe)_nO_3n+2 (n = 5 and 6). Acta Crystallogr. B, 69(2):137--144, 2013.

[2] A. Manan, Y.Iqbal, and I. Qazi. Phase, microstructural characterization and dielectric properties of ca-substituted Sr₅Nb₄TiO₁₇ ceramics. J. Mater. Sci., 46:3415--3423, 2011.

[3] Y. Koval, F .Chowdhury, X. Jin, Y. Simsek, F. Lichtenberg, R. Pentcheva, and P. Muller. Resistive memory switching in layered oxides: A_nB_nO_3n+2 perovskite derivatives and Bi₂Sr₂CaCu₂O_8+δ high-T_c superconductor. Phys. Stat. Sol. A, 208:284--299, 2011.

[4] F. Lichtenberg, A. Herrnberger, and K. Wiedenmann. Synthesis, structural, magnetic and transport properties of layered perovskite-related titanates, niobates and tantalates of the type A_nB_NO_3n+2, A'A_k-1B_kO_3k+1 and A_mB_m-1O_3m. Progr. Sol. Stat. Chem., 36:253--387, 2008.

[5] A. Wölfel, F. Lichtenberg, and S. van Smaalen. Two-dimensional clusters in La_n(Ti_1-xFe_x)_nO_3n+2 (n = 5 with x = 0.2 and n = 6 with x = 0.33). J. Phys. Condens. Matter, 25:076003, 2013.